Abstract
ここでは、ロドリゲス回転行列の導出過程を記載する。
Derivation
出発点として、以下の命題は真である。
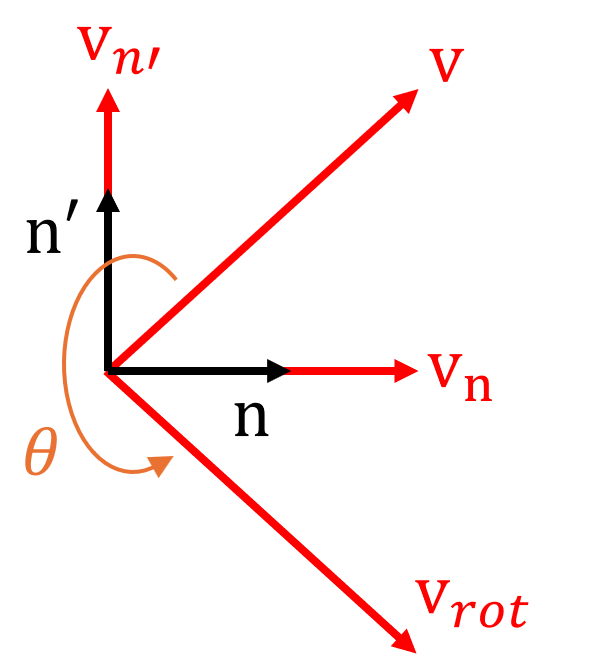
$\mathbf{v}_{rot}$は、任意ベクトル$\mathbf{v}$が単位ベクトル\(\mathbf{n}\)周りに\(\theta\)回転したものである。
回転軸\(\mathbf{n}\)と、それに垂直な単位ベクトル\(\mathbf{n}'\)それぞれの方向に\(\mathbf{v}\)を分解すると
$$ \mathbf{v_n} = (\mathbf{n}\cdot \mathbf{v})\mathbf{n} $$\((\mathbf{n}\cdot \mathbf{v})\)は\(\mathbf{v}\)のn軸方向成分のスカラーであり、 nは単位ベクトルなので、そのまま掛けることでベクトルに戻している